[ベスト] 五角星面積 公式 247671

 正多角形の面積を考えるときの基本的な考え方は 三角形に分割すること です。 正三角形についてそれ以上分割することができないので今回は省きたいと思います。 では正四角形（Created Date PM 外角・内角の和、面積、対角線の公式と求め方 21年12月25日 この記事では、「多角形」についてわかりやすく解説していきます。 多角形に関するさまざまな公式（外角の和・内

Excel利用公式制作星星图的详细方法 百度经验

五角星面積 公式

五角星面積 公式-C = T X (2rh 112) —m L(rh) h x L(r) < T x (2rh 112) < h x L(r h) L(r) It Tr x 2r) Zo h Tr x x h) (å)X0 L(r) < x 2r < L(r) 4 (i) (iii) 92 (11) Il David Garber and Boaz Tsaban, A Mechanical 已知五角星的顶角大小为36度，则三角形的面积St=1/2×a×a×sin（36度）≈2939cm^2 五边形的边长b=2*a×sin（18度）≈618cm S5=5*1/2*b*b/2*tan (54度)≈6572 cm^2 总面

计算任意五角星与圆的相交面积 C Qq 的博客 Csdn博客 圆和五角星面积比

 3 ベクトルの平行四辺形の面積公式 三角形oabの面積をベクトルを用いて表せたら、平行四辺形oacbの面積も簡単に導出できます。 平行四辺形の対角線を引くと、合同な三角形が 2 正五角形の面積は 2倍角の公式より あとは三角関数の中身を計算すればよい。 （正五角形の図は下にもあるので適宜参照してください） AB=aとし，AからBEにおろした垂線の足をKもくじ 1 sinθで三角形のたての長さと面積を計算する 11 多角形の面積の計算方法;

多角形の面積を計算する的な GitHub Gist instantly share code, notes, and snippets正五角形の面積 正五角形の面積 中三程度で理解できるように、根号と三平方の定理までを使用し、三角関数は使用していません。 三角関数で解く場合は こちら を参照してください。 1）外接円 标准的正五角星，10条边一样长，已知变长为a （a=10 cm），所以周长：C=10a=100cm 面积：已知五角星的顶角大小为36度，则三角形的面积St=1/2×a×a×sin（36度）≈2939cm^2 五边形的边长b=2*a×sin（18度）≈618cm S5=5*1/2*b*b/2*tan (54度)≈6572 cm^2

Alpinestars has outfitted countless world champions and produces the highest level of performance and protective footwear and apparel for motorcycle, motocross and mountain bikePentagram is the world's largest independent design consultancy The firm is owned and run by 24 partners, each of whom are leaders in their individual fields三角関数を使って三角形の面積を求める公式もあります。 三角形の面積 S=1/2・a ・b sinθ aは底辺の長さ、b sinθは三角形の高さです。

五边形 百度百科

五角星面积公式怎么算 搜狗图片搜索

正多角形の面積 中学入試の答えを知るため。 （02角形の対角線の本数） sqrt (xx) のように指定してください。 正多角形の1番長い対角線の長さを表示してほしい。 1辺を1としたときと仮定し 五角星是最简单的规则星形多边形。 正五角星形的和弦切片的黄金比例为。 输入一个值，然后选择小数位数。 然后单击计算 内体：边长为c的规则五边形 顶角：等腰三角形，腿长为b，底以下の公式があります。 角柱・円柱の体積 = 底面積 × 高さ 底面積と高さが分かっている場合、それぞれの掛け算によって角柱や円柱の体積を計算できます。 角錐や円錐の体積の公式はこれと似て

五角星面积公式怎么算 搜狗图片搜索

五角星面积公式怎么算 搜狗图片搜索

LINE 今回の記事では、 上のような2パターンの 正八角形の面積を求める方法 について解説していきます。 この問題を解くためには中学3年生で学習する「三平方の定理」の知識が必要となります它是利用三角形的三条边的边长直接求三角形面积的公式。 表达式为：S=√p (pa) (pb) (pc)，它的特点是形式漂亮，便于记忆。 相传这个公式最早是由古希腊数学家阿基米德得出的，而因为这个公式2 ヘロンの公式で面積を計算する 21 余弦定理を使い、ヘロンの公式を無視する;

愛轉角 圣誕節手工高密度泡沫五角星紙手工diy 超輕粘土填充裝飾材料創意材料包 Yahoo奇摩拍賣

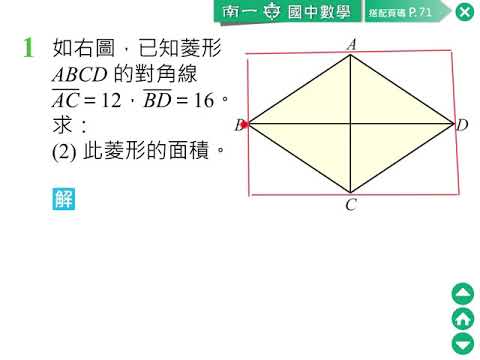
習作 菱形與箏形1 2 八年級下冊 110舊版 均一教育平台

星形の内角の和が180°になる理由 星形の角度が180°になる理由を説明していくために 三角形の外角の性質を知っておく必要があります。 このように 三角形の外角は、隣にない内角2つ分を合わせ角錐・円錐の体積 はじめに角錐・円錐の体積について解説していきます。 体積はどちらも 『体積＝底面積×高さ×1 3 1 3 』 となります。 このときの "高さ" とは、 頂点から底面に下ろした垂線如果已经知道这个长度，你可以使用下面这个简单的公式。 正五边形的面积= "pa"/2，其中"p" = 周长，"a" = 边心距。 如果不知道周长，可以通过边长来计算。计算公式是：p = 5s，其中"s"是边长。

平面凸五邊形最大面積與圓內接2n 1 邊形的正弦公式

Q Tbn And9gcsfyxeqddm7ehysp Afoumi Q1z Dx3mg8lknhln9o5zyrjravwi5jj Usqp Cau

正十五角形 正十五角形においては、中心角と外角は24 °で、内角は156°となる。 一辺の長さが a の正十五角形の面積Sは = = ( ) (/) は有理数と平方根の組み合わせのみで表せる = = ( ) 正十This Pin was discovered by Youko Oohata Discover (and save!) your own Pins on 星の形状が、正五角形の対角線を結んでできる形状の場合には、 星の1辺（10辺ある部分のことです）の長さをa、星の面積をSとすると、 S=5 (1/tan36° sin72°)a^2 ≒a^2 で求

五角星面积公式怎么算 搜狗图片搜索

小學數學三角形 Top 300件小學數學三角形 22年11月更新 Taobao

 ひし形の面積の公式は 「たての対角線の半分の長さ」と「横の対角線の半分の長さ」の直角三角形の 4倍 と考えると分かりやすいです。 「たての対角線の半分の長さ」と「横の対角線 三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求面積 內角（度） 108° 內角和 540° 特性 凸、圓內接多邊形、等邊多邊形、等角多邊形、等邊圖形

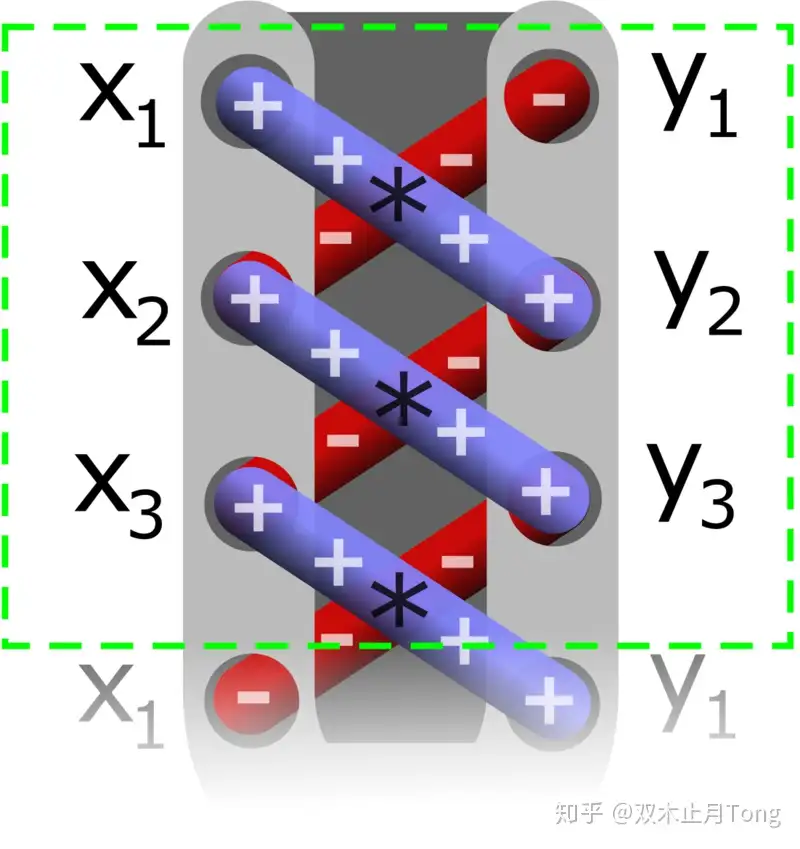
国际数学竞赛 任意多边形面积计算公式 知乎

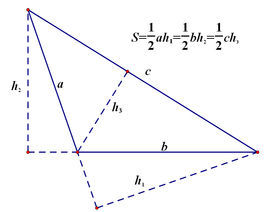
三角形面積公式 三角形面積公式是指使用算式計算出三角形的面積 同一平面內 百科知識中文網

面積 Wikiwand

面積 Wikiwand

计算花瓶形的面积 Page106 青岛版九年级数学上册电子课本 教材 教科书 好多电子课本网

五角星计算公式 Csdn

课堂实录 组合图形的面积 五上

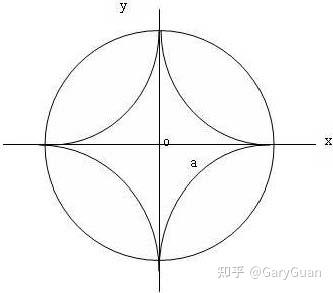
星形线所围成图形的面积 知乎

五角星面积计算公式 西瓜视频搜索

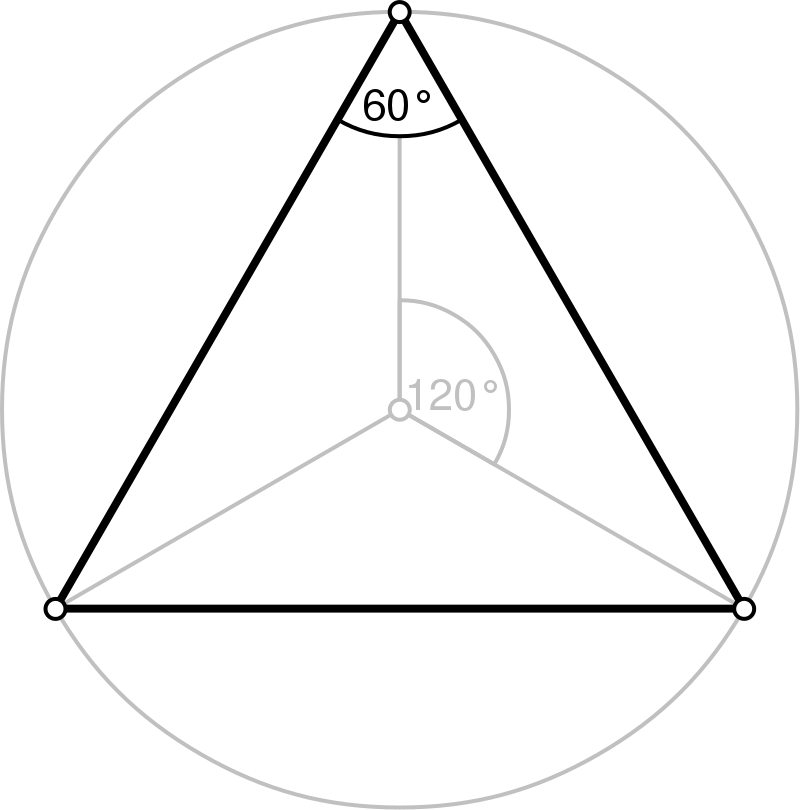
正三角形 维基百科 自由的百科全书

巧用外角求五角星内角和 哔哩哔哩

苏科版九年级下册6 2 黄金分割课堂检测 教习网 试卷下载

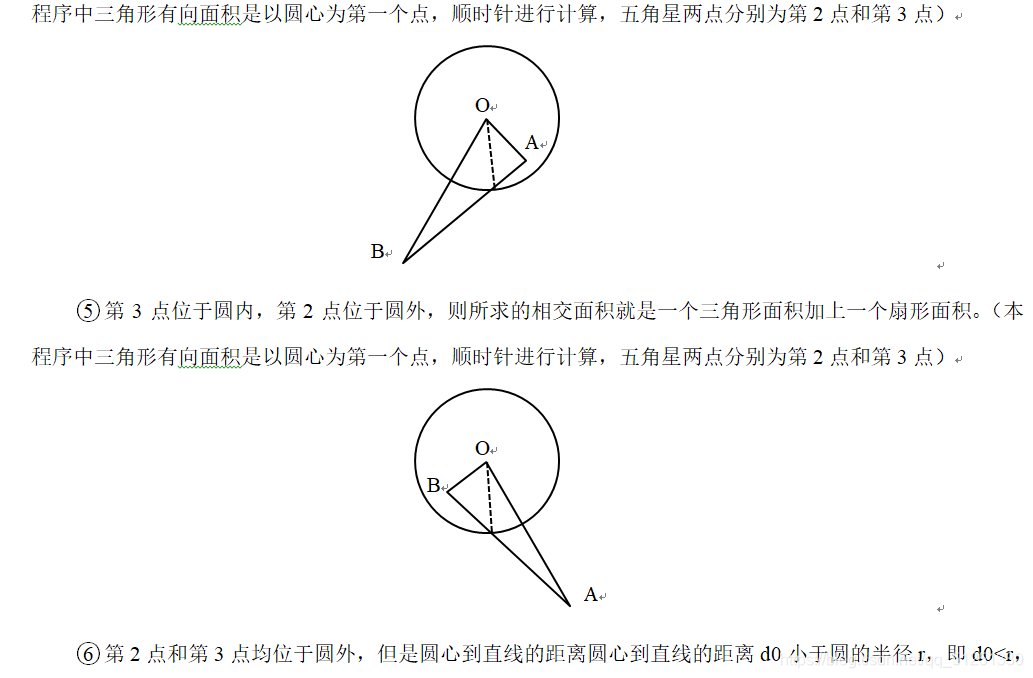
计算任意五角星与圆的相交面积 C Qq 的博客 Csdn博客 圆和五角星面积比

0615 正十二芒星的面積是多少 Youtube

五角星面积公式怎么算 搜狗图片搜索

Excel利用公式制作星星图的详细方法 百度经验

五角星面积公式怎么算 搜狗图片搜索

Wps神技能 如何在excel表格中计算圆的面积 腾讯云开发者社区 腾讯云

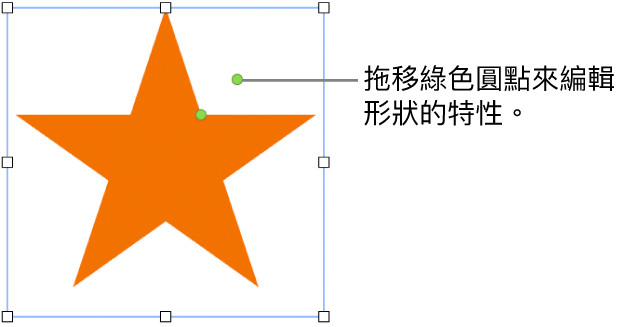
在mac 上的numbers 中加入並編輯形狀 Apple 支援 香港

五角星面积计算公式 西瓜视频搜索

简单的五角星的面积公式讲解 哔哩哔哩

Q Tbn And9gcrtfkotxgng Yd Eflkpdrd3amlliimgigx Wrrpctwcenjjixpygrl Usqp Cau

Wps神技能 如何在excel表格中计算圆的面积 腾讯云开发者社区 腾讯云

学习做五角星 哔哩哔哩

几何图形三角形 Top 300件几何图形三角形 22年12月更新 Taobao

计算任意五角星与圆的相交面积 C Qq 的博客 Csdn博客 圆和五角星面积比

Polygon 演算法筆記

五角星面积计算公式 西瓜视频搜索

正n 角星的內角和探討

正n 角星的內角和探討

Wps文档如何画空心五角星 百度经验

Q Tbn And9gcqckejhqpgscejewcmd4nbhyyufalfzdicdoceyezr5i Sh Z Vq Usqp Cau

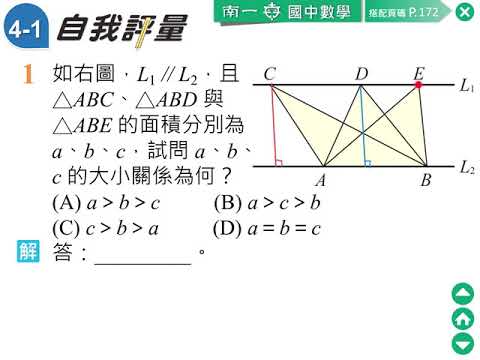
評量 平行線之間的三角形面積比較 八年級下冊 110舊版 均一教育平台

五边形 维基百科 自由的百科全书

计算任意五角星与圆的相交面积 C Qq 的博客 Csdn博客 圆和五角星面积比

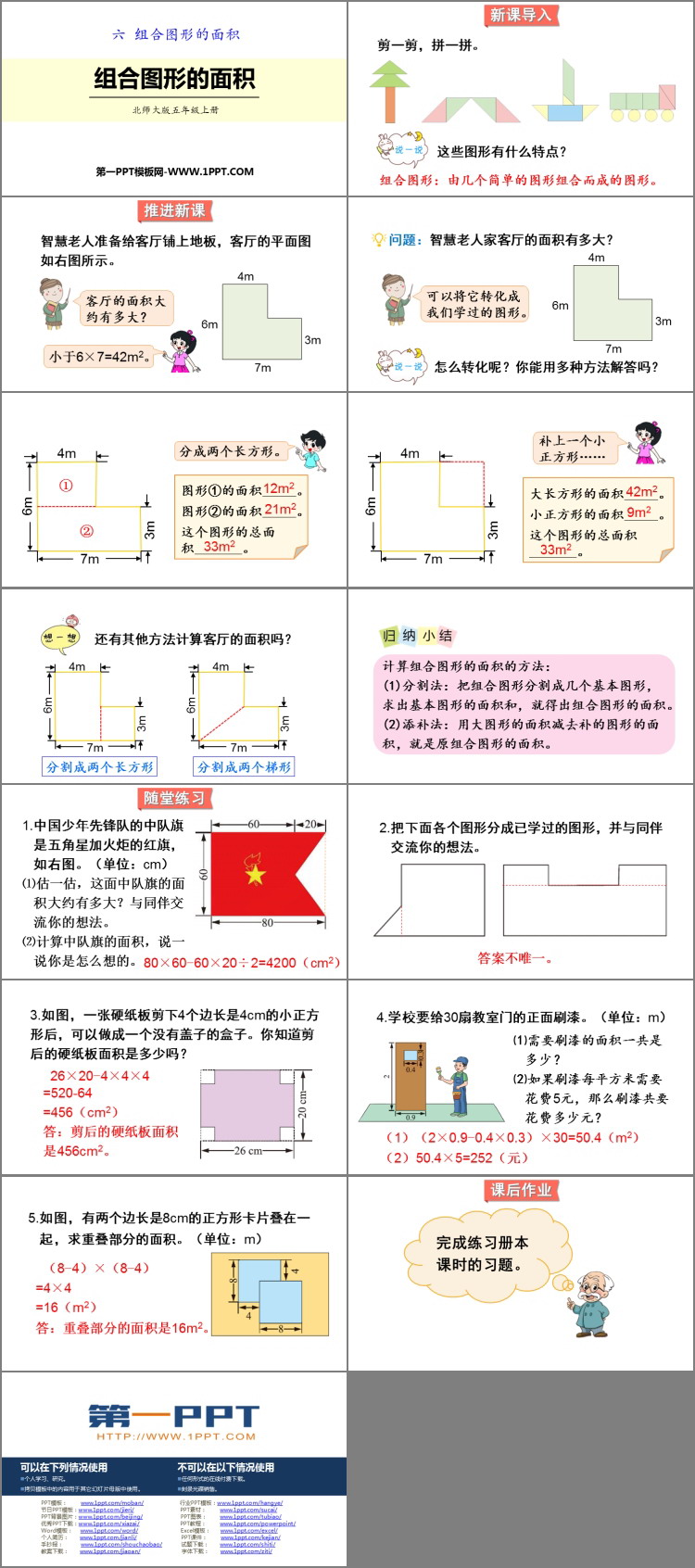
组合图形的面积 组合图形的面积ppt课件下载 第一ppt

浙江省嘉兴市海盐县重点达标名校22年中考数学全真模拟试题含解析 教习网 试卷下载

22 23学年河北省邯郸市魏县人教版八年级 上 期中数学试卷 解析版 教习网 试卷下载

3种方法来求五边形的面积

3种方法来求五边形的面积

3种方法来求五边形的面积

環形 維基百科 自由的百科全書

国际数学竞赛 任意多边形面积计算公式 知乎

Android 五角星画法五角星计算公式 月落西楼的博客 Csdn博客 画五角星的公式

组合图形的面积 组合图形的面积ppt下载 第一ppt

平面凸五邊形最大面積與圓內接2n 1 邊形的正弦公式

例題 平行四邊形中的面積關係 1 八年級下冊 110舊版 均一教育平台

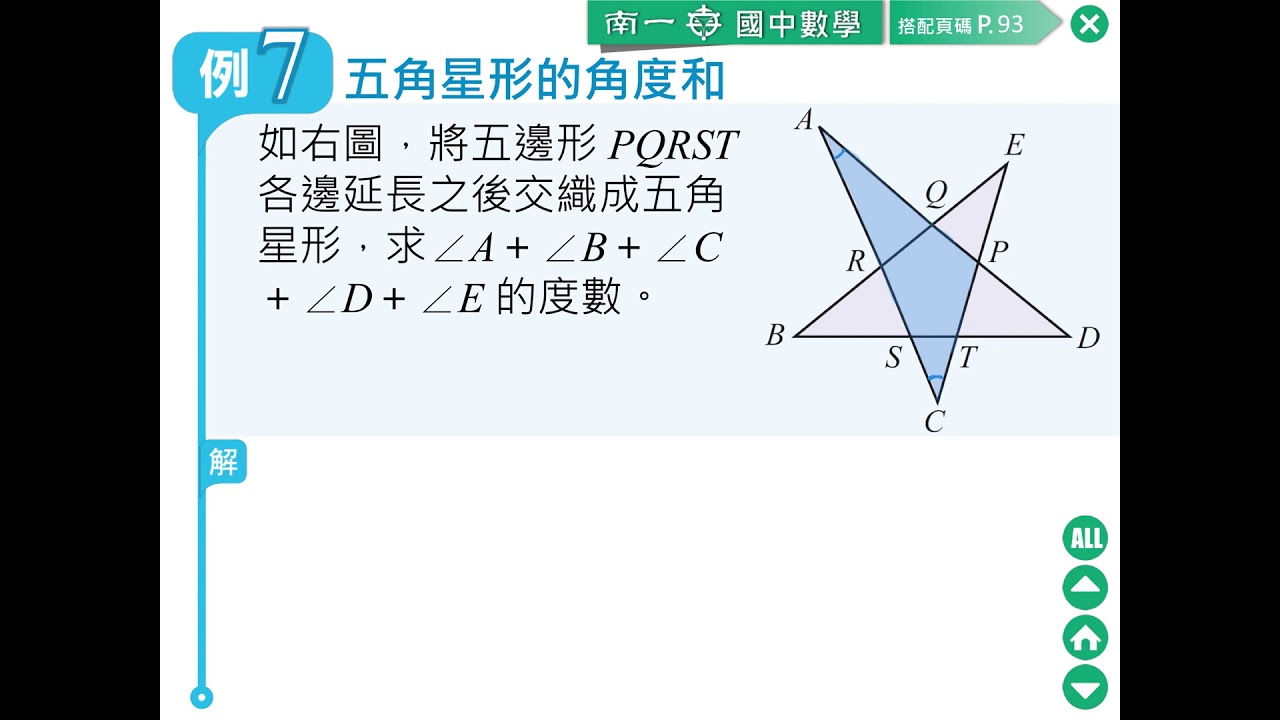
例題 五角星形的角度和 數學 均一教育平台

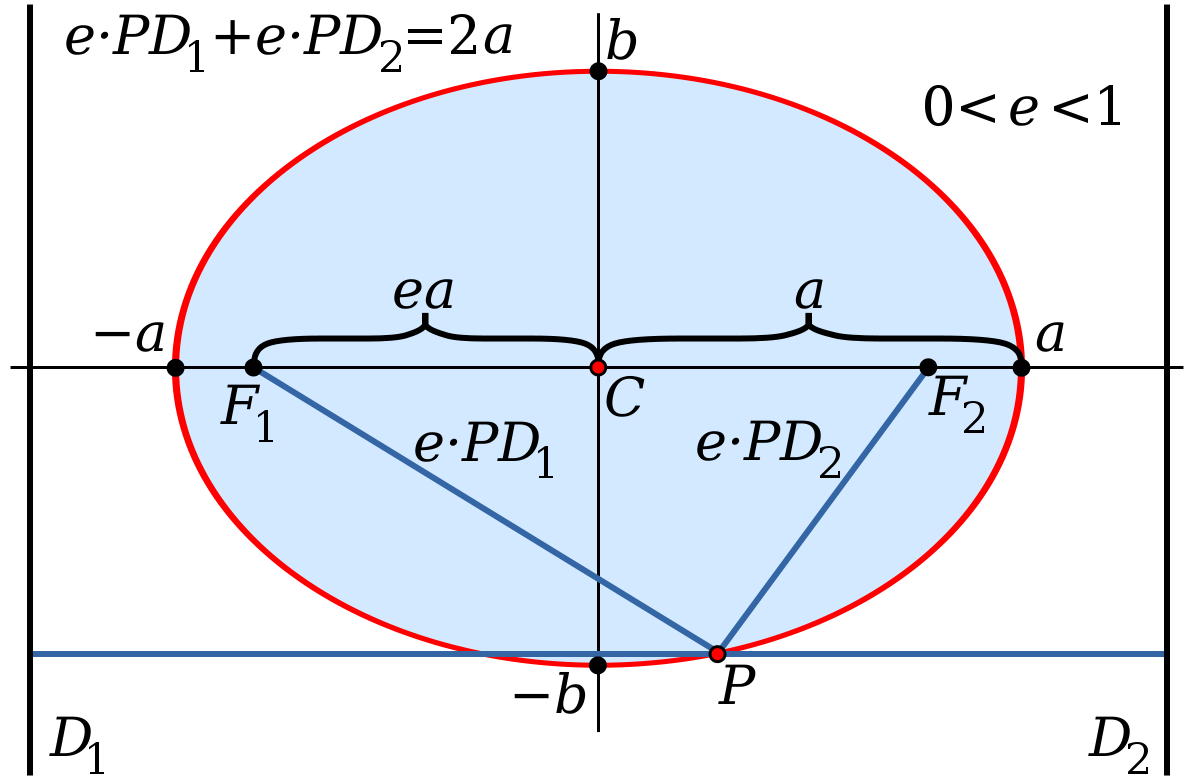
橢圓 維基百科 自由的百科全書

3 6 弧长和扇形面积的计算 Page104 青岛版九年级数学上册电子课本 教材 教科书 好多电子课本网

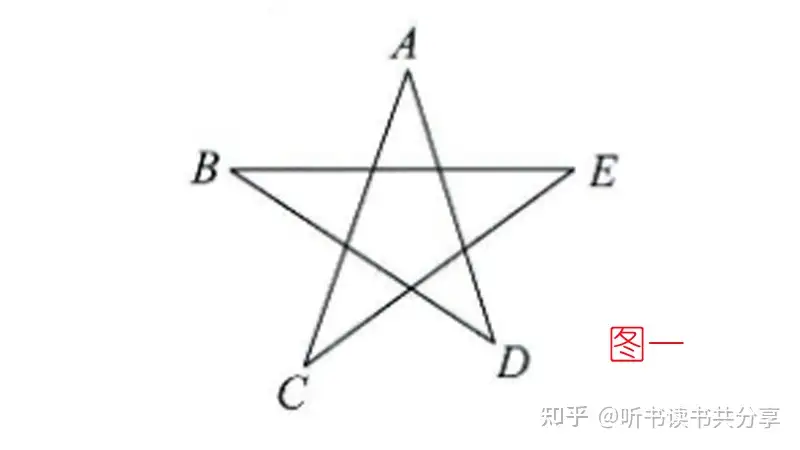
一个 8字模型 搞定五角星五个顶角度数之和 知乎

度量 大小和形状 在苏州的城边 博客园

兩分鐘學會星星型角度計算 劉豪老師 Cc字幕 Youtube

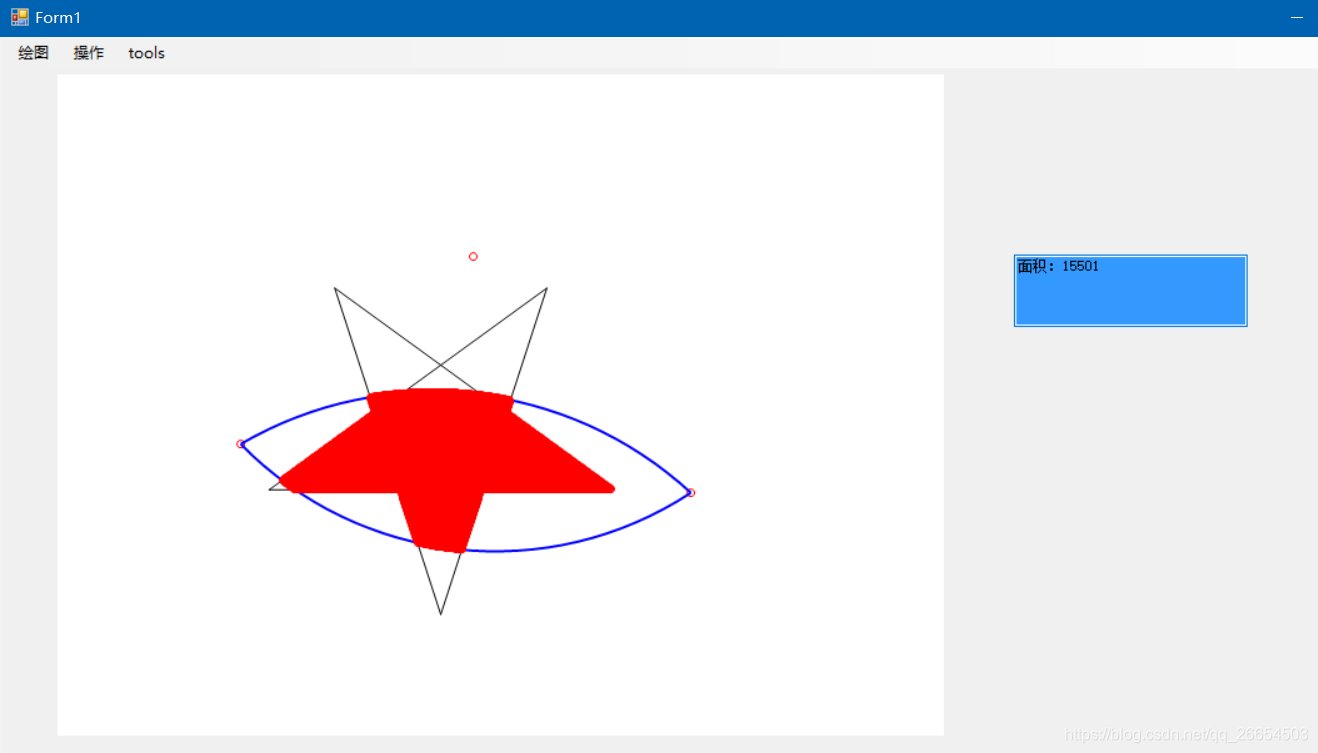
C 画五角星 月牙形和它们相交求面积 一秋 1024的博客 Csdn博客 C 计算几何求面相交

五角星面积计算公式 西瓜视频搜索

组合图形的面积 组合图形的面积ppt 第一ppt

五边形 Wikiwand

3种方法来求五边形的面积

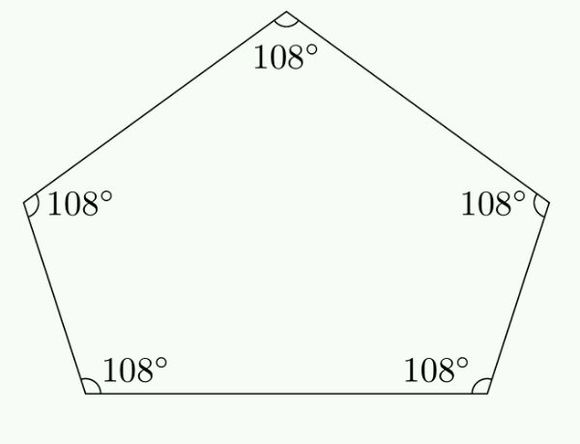
正五邊形 定義 面積公式推導 內切圓半徑 構造 物理方法 畫法 常規畫法 尺規作圖 中文百科全書

综合与实践黄金分割与五角星 黄金分割点 Page159 青岛版九年级数学上册电子课本 教材 教科书 好多电子课本网

在ipad 上的numbers 中加入並編輯形狀 Apple 支援 香港

Wps神技能 如何在excel表格中计算圆的面积 腾讯云开发者社区 腾讯云

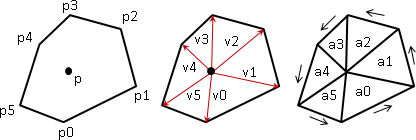
Polygon 演算法筆記

Education 1253

3种方法来求五边形的面积

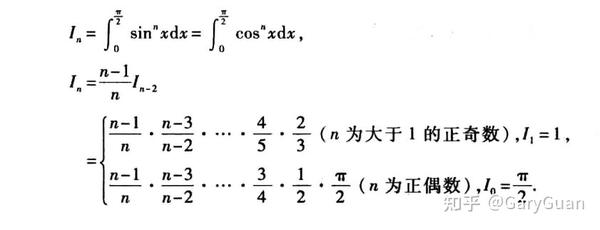
星形线所围成图形的面积 知乎

方形图角 Top 58件方形图角 22年12月更新 Taobao

五角星面积计算公式 西瓜视频搜索

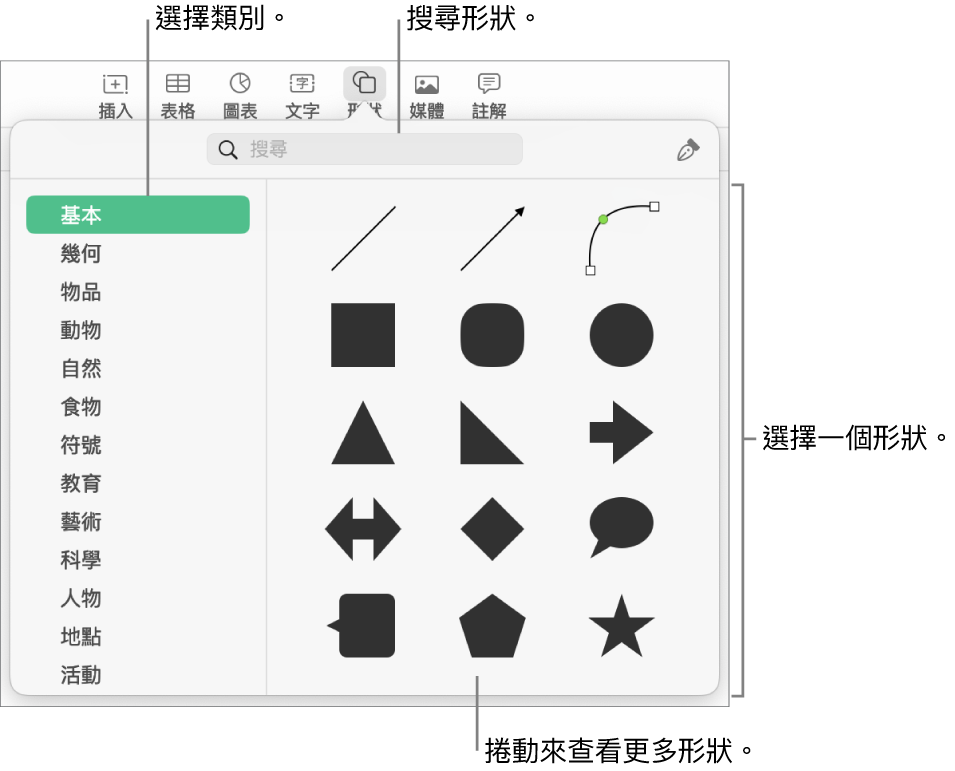
在mac 上的numbers 中加入並編輯形狀 Apple 支援 香港

长方形几何片 Top 0件长方形几何片 22年11月更新 Taobao

三角形教具 教具 教學輔助 科學生活 人氣推薦 23年1月 露天市集

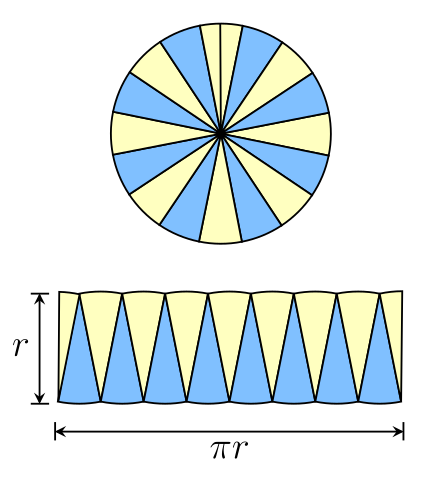
面積 Wikiwand

课堂实录 组合图形的面积 五上

正n 角星的內角和探討

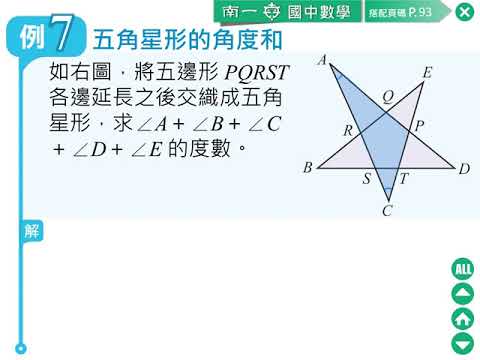
例題 五角星形的角度和 數學 均一教育平台

3种方法证明 为什么五角星顶点的内角和是180 哔哩哔哩

五边形 Wikiwand

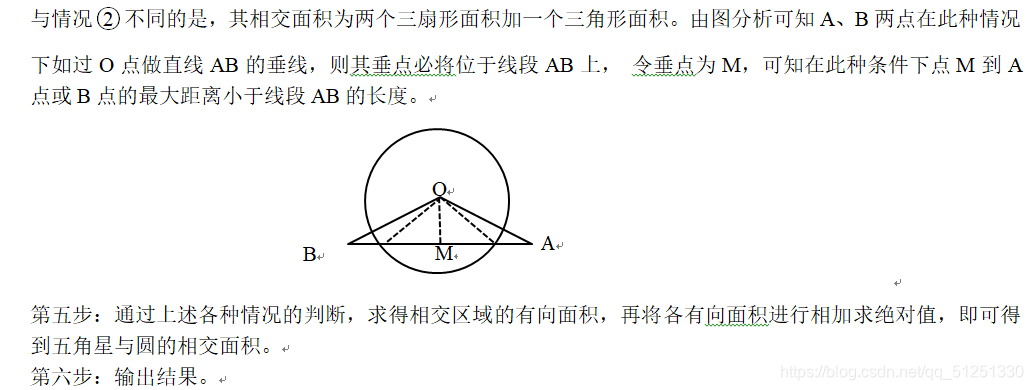
计算任意五角星与圆的相交面积 C Qq 的博客 Csdn博客 圆和五角星面积比

几何画板同心五角星与五边形的变换

平面凸五邊形最大面積與圓內接2n 1 邊形的正弦公式

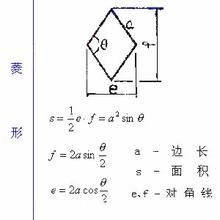
菱形面積公式 菱形面積公式就是由三角形面積公式得來的 菱形面積 兩個三角 百科知識中文網

提高奥数逻辑思维能力 寻找公式 思维拓展网

五角星面积计算公式 西瓜视频搜索

觀念 正三角形的高與面積 八年級下冊 110舊版 均一教育平台

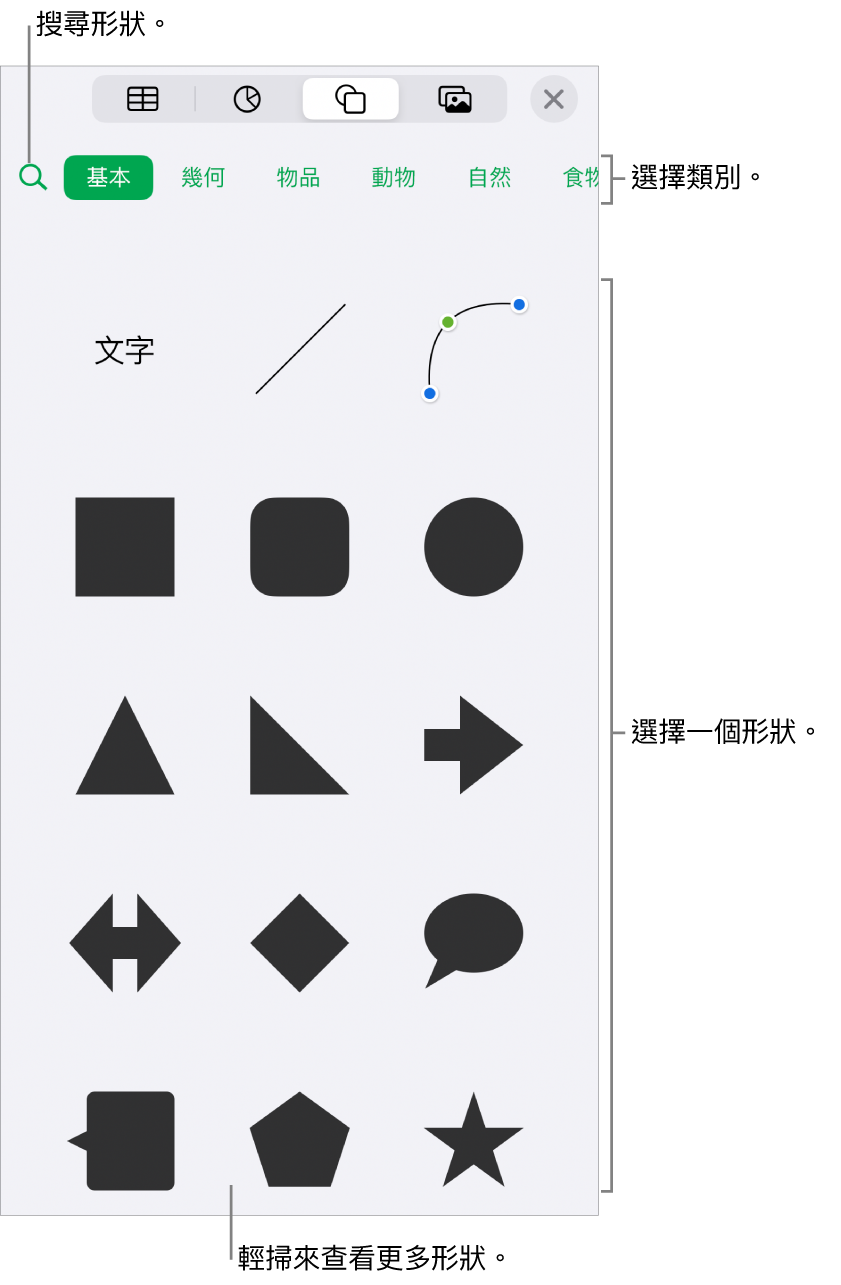
在iphone 上的numbers 中加入並編輯形狀 Apple 支援 香港

五角形 新人首单立减十元 22年5月 淘宝海外

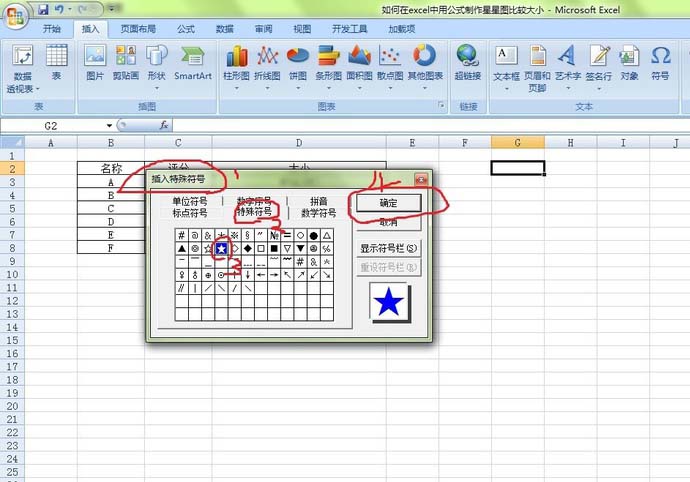
Excel怎么利用公式制作星星图 伙伴云

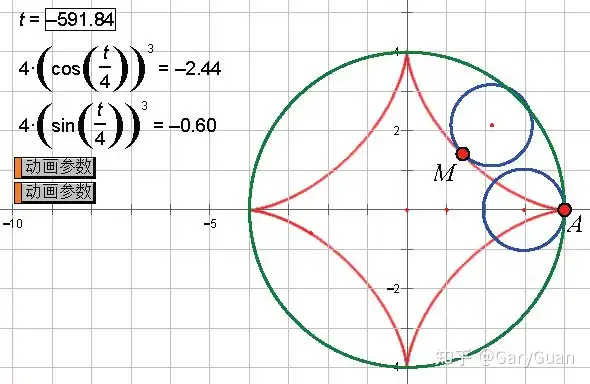
星形线所围成图形的面积 知乎

五角星面积公式怎么算 搜狗图片搜索

愛轉角 水晶滴膠金屬邊框uv滴膠手工制作飾品異形配件模型套裝五角星邊框 模具 飾品類 Yahoo奇摩拍賣

巧妙嵌入 黄金 成就试题 精彩 参考网

Q Tbn And9gcsmfirurluaqcax4xmrmorqvsqcinopqwc9murivlkgfsljvyjgsmiy Usqp Cau

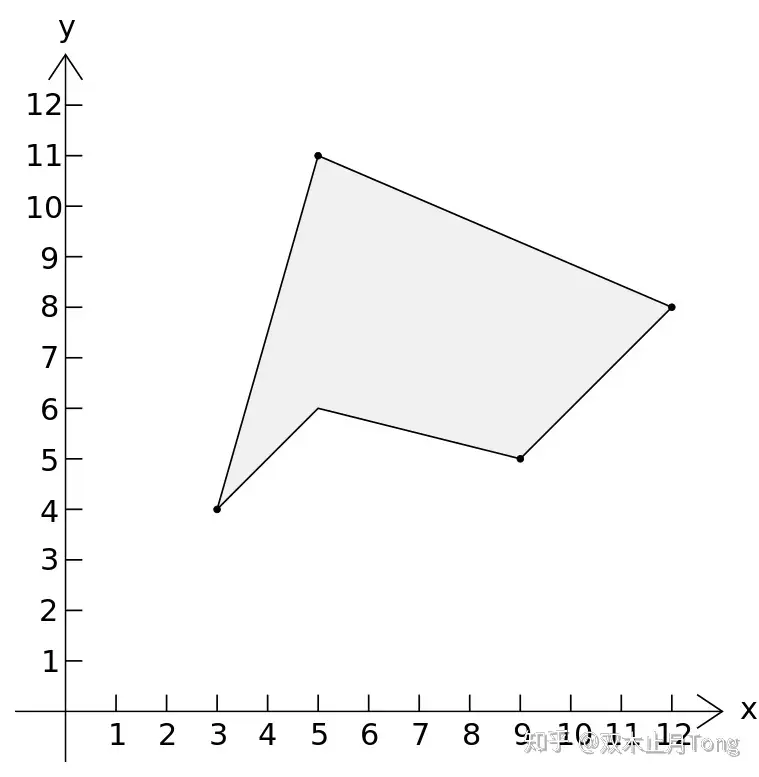
国际数学竞赛 任意多边形面积计算公式 知乎

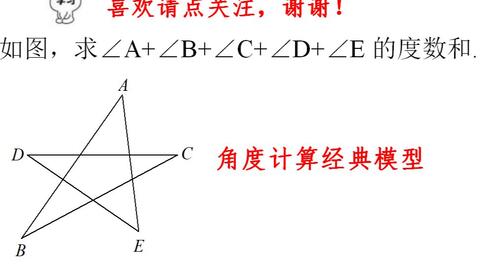
一个角度都没有 怎么求五角星5个顶角和 看完视频 这么简单 哔哩哔哩